Understanding margin of error in surveys.

Margin of error is a term commonly used in market research but often not very well understood.
However, it has a significant impact on the accuracy of the conclusions you can draw from a survey.
The concept behind it is nuanced and slightly complex so read on as we attempt to simplify it for you!
While we won't dive into how to calculate the margin of error (there are quite a few online calculators available without having to work it out yourself), we hope that at the end of this piece you have a better understanding of what margin of error is and what are the factors that affect it.
So what is margin of error?
Simply put, margin of error tells you how precise are the results you obtain from a survey. Or in other words, as the name suggests, how much of a room there is for error.
But why should there be any room for error in the first place?
When you conduct a survey, you are only talking to a subset of the population you want to draw conclusions about.
For instance, if you want to know what percentage of a country owns dogs, you might survey only a n = 1000 sample of respondents rather than the entire population.
It is reasonable to assume that the results you get from this survey of n = 1000 respondents won’t exactly match the “true” results you would get if you surveyed the entire population.
This is where margin of error comes in.
The margin of error tells you how close you can expect your results to be compared to the “true” population value. For instance, if your results indicate that 20% of the population owns a dog in a survey with a margin of error of 3%, it means your results can be plus or minus 3 percentage points away from the “true” population value i.e. within the range of 17% to 23% .
The narrower the margin of error the more certain you are that the results of your survey are reflective of the opinions and behaviour of the overall target population.
Now how do you work towards your desired margin of error? For that you need to know what factors affect it.
Factors that influence margin of error
Margin of error is a derived metric that depends on three factors : population size, sample size, and confidence level. We elaborate on each of these below.
1. Population size
The term population refers to the entire target group of people you want to study with your survey.
In the above example of dog ownership, the population of interest is the entire population of a country.
However, if in a survey you want to study the opinions or behaviour of a subgroup, say millennials in a country, the population in this example would be the total number of millennials in that market. Margin of error may vary depending on the population size your survey aims to study.
2. Sample size
While the population size is a fixed number beyond your control, sample size is the most important factor that researchers have to make a decision about while designing a survey because it has a significant impact on the margin of error.
There is an inverse relationship between the margin of error and the sample size : as the sample size increases, the margin of error decreases. And this is logical because the more people you survey, the more confident you can be that your results are closer to the “true” population value (keeping in mind that the survey does not have other biases of course).
However, an important point to take note of is that while the reduction in margin of error is considerable as you increase the sample size till n = 1000, there is a diminishing return when you go further up. It is often not worthwhile for researchers to devote additional time and money to collect more than n= 1000 samples as the margin of error does not considerably decrease below 3% after that.
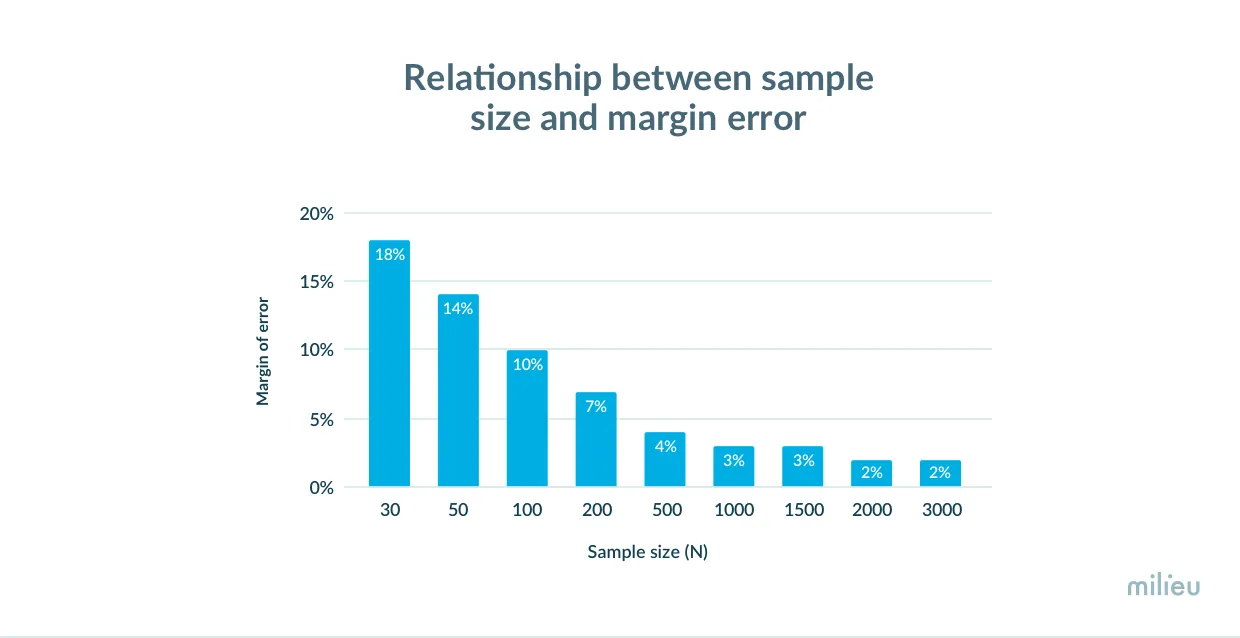
For a more detailed lowdown on how to decide on an optimal sample size for your survey, you may refer to this article.
3. Confidence level
Confidence level denotes the probability with which the range of values estimated by the margin of error consists of the “true” population value.
This means that even though the statistical calculations behind margin of error will produce a range of values which includes the “true” value, there is no 100% guarantee that the calculation is accurate all the time. There is a slight chance that the range may not include the “true” value.
The confidence level tells you how confident you can be that your margin of error range will include the true result.
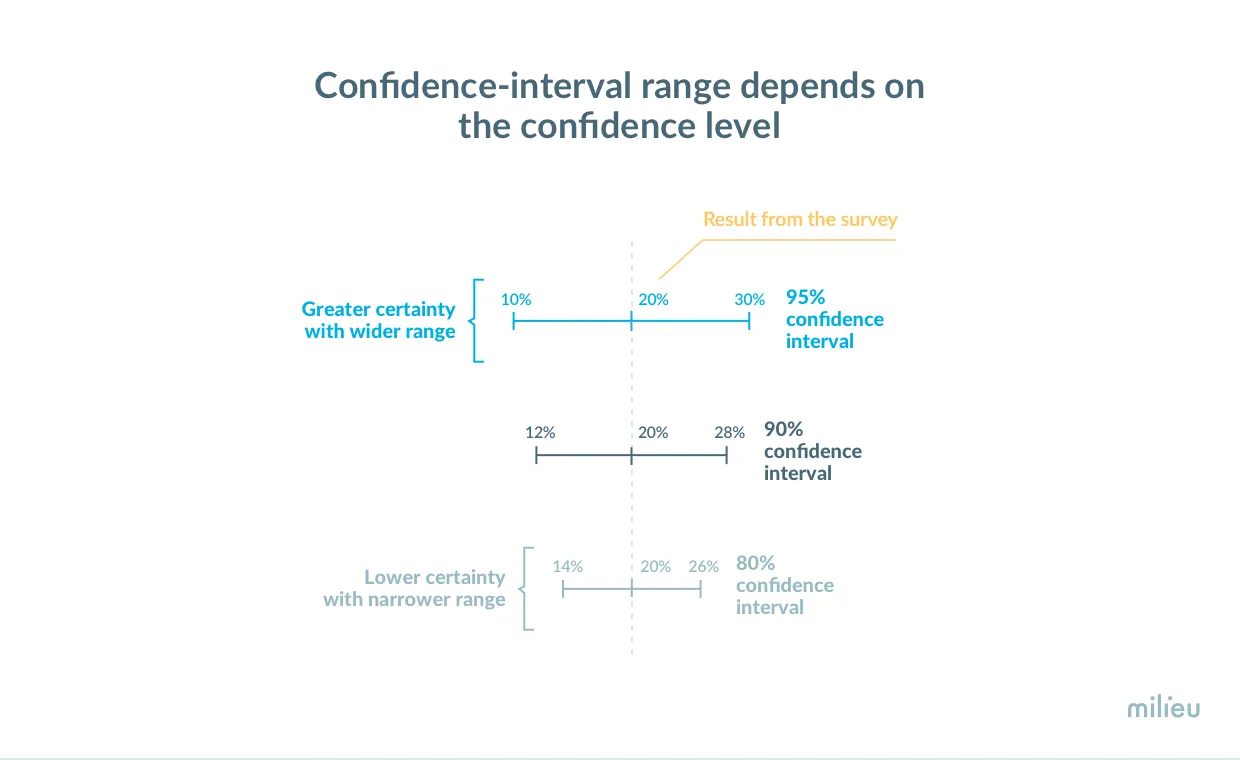
You may have noticed that when reporting the margin of error, there is always a confidence level attached to it. For example : the margin of error for this survey is 5% at the 95% confidence level. This means that if you were to conduct the survey 100 times, 95 of those times you would expect the result to be within 5 percentage points of the true population value.
While 95% is the typical choice of a confidence level in market research, it is not uncommon to see a 90% confidence level or sometimes lower. The question you might ask is : why not always go for a higher confidence level if it gives you more certainty? The reason being it comes at a cost.
To give you an example, if you surveyed n = 100 respondents and find that 20% of them are smokers, the margin of error is 6% at an 80% confidence level. In other words, the “true” percentage of smokers can range between 14% and 26%. However, if you change the confidence level to 95%, the margin of error increases to 10%, making the error range wider. If you want to bring down the margin of error to 6% at a confidence level of 95%, the solution would be to recruit more respondents. By bumping up the sample size to n = 230, you can now achieve a 6% margin of error at 95% confidence level. While this may be feasible in some instances, additional recruitment of respondents may come at an increased cost and time.
To summarise, a lower confidence level gives you a lower margin of error, but with a higher probability that the range doesn’t consist of the actual value. A higher confidence level leads to a wider margin of error at the same sample size. The higher the confidence level, the wider the margin of error because it allows you to be more confident that the “true” population value lies within the +/- percentage interval.
Conclusion
Data collected from a survey will never perfectly represent the behaviour and opinions of the target population as a whole. How much room there is for error is contingent on the three factors outlined above : population size, sample size, and confidence level.
Ideally, the margin of error should not be an afterthought that’s calculated post survey fieldwork. It is good to design the study keeping in mind the level of accuracy that is desirable and sample size is the most important determinant of the margin of error.
If cost, time, and feasibility are not barriers, researchers often aim for higher sample sizes close to n = 1000 so that the margin of error is low. However, if there are resource and operational constraints, one has to often work with lower samples, thus increasing the margin of error.
It is important to keep in mind the objective of the study. If it is crucial to get as precise results as possible because of important implications (e.g., election polls, government-led surveys with policy implications) then it is imperative that you keep the margin of error as low as possible. However, sometimes surveys are used just to get a rough sense of responses or opinions (e.g., customer feedback surveys, feedback on early stage product designs) where any feedback is valuable and representativeness of the entire population is not of utmost importance - here one may be comfortable with a higher margin of error.
Milieu Insight, an award-winning online survey tool and market research company, champions businesses in leveraging data for success.
Exploring the evolution of online brand research, our brand health research guide emphasizes engaging diverse audiences and employing adaptable methodologies to yield comprehensive insights.

.avif)



.webp)

