A complete guide to significance testing in survey research

When it comes to survey results, we mostly deal with percentages or proportions.
- 90% of customers said they were satisfied with the quality of our brand
- 52% of respondents confessed that they've followed an influencer's advice on DIY beauty hacks, only to regret it
- 60% of Gen Zs would rather be stung by bees than return to the office
Surveys are often used to understand differences between various groups of people or products.
For example, an insights team might want to know whether the difference in brand awareness between two products is statistically significant, or whether the difference in customer satisfaction between age groups is meaningful.
As a result, it is common to report survey findings supported by statistical significance tests and p-values.
Although statistical analysis tools and calculators automate the calculation of significance tests without going into the nitty gritty details, it is important to have a good theoretical understanding in order to better interpret the results and recognise its limitations to prevent its misuse.
This article offers an overview of the fundamentals of significance testing.
Let’s start with an example
Since statistical concepts can be challenging to understand, let’s contextualize it with a common use case in market research.
Imagine you're conducting a Campaign Effectiveness Study in Singapore.
A brand plans to run video advertisements on various media channels, and you want to see if people's perception about the brand changes after the campaign.
To assess the campaign’s effectiveness, surveys are conducted with two distinct groups of people namely, a pre-campaign survey group (Group 1) of 500 respondents and a post-campaign survey group (Group 2) of another 500 respondents.
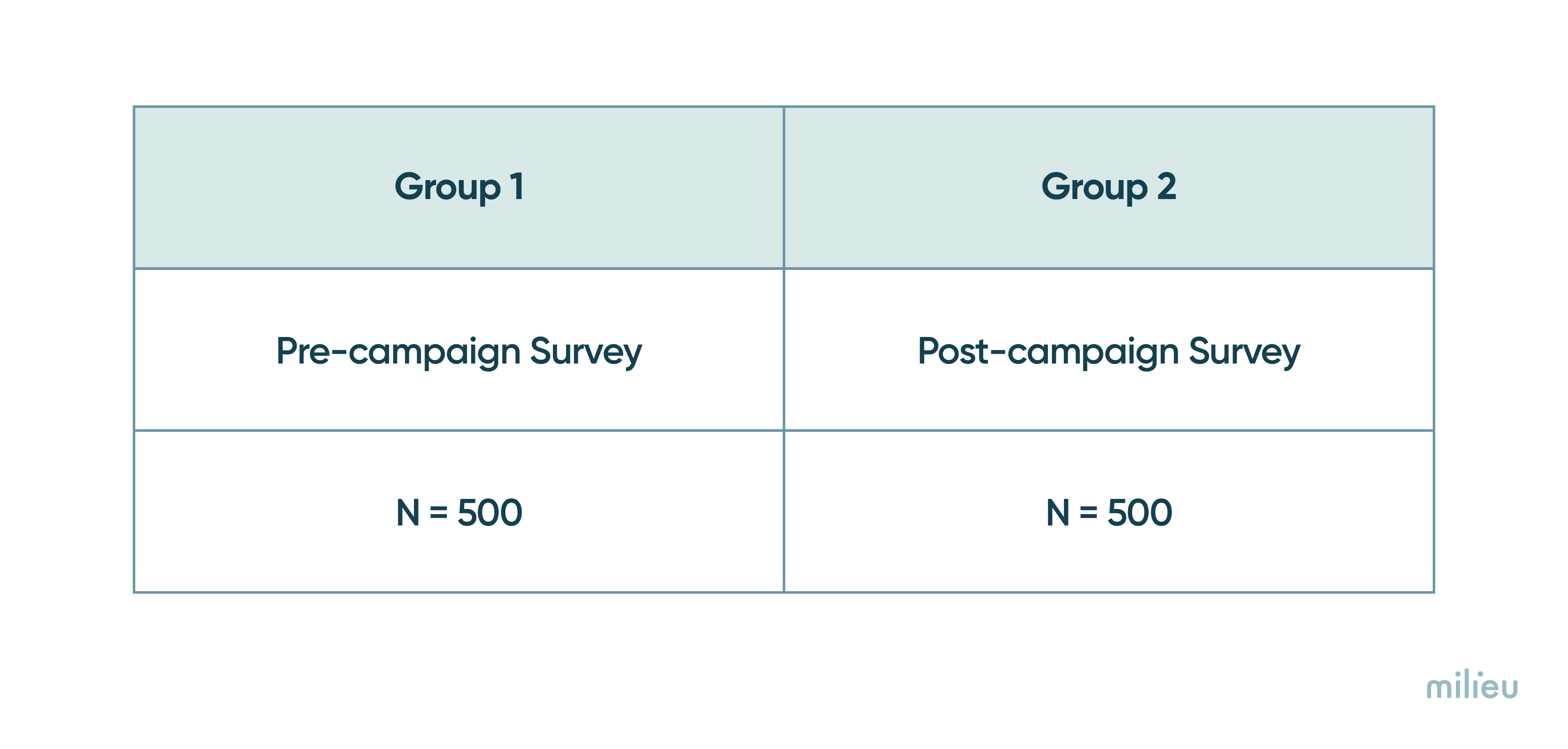
The results of the two surveys are then analyzed to identify any differences in how people perceive the brand before and after the campaign. Metrics such as awareness, familiarity, usage, purchase intent, and brand attributes are used to measure these changes.
So what’s the issue?
You observe that brand awareness stood at 30% in the pre-campaign survey, but increased to 39% in the post-campaign survey.
To the naked eye, the numbers are obviously different. But a discerning eye might ask :
- Are the differences observed actually meaningful (possibly due to the influence of the advertisement campaign) OR
- Are the numbers different due to random chance? While there is a difference, we need to be sure if these differences are merely a coincidence, because of the particular subset of people you happened to survey, or if they genuinely reflect differences in the entire population represented by our sample.
This is where significance testing comes to play.
What is significance testing?
The key objective of significance testing is to interpret differences. It is a set of statistical tools that help us determine whether the differences we observe in our data are real and representative of the entire target population, and are unlikely to have occurred by chance.
You may also come across other terms that describe the same concept: “hypothesis testing” or “tests of statistical significance”.
Significance testing in survey research are broadly done in two different contexts :
- Hypothesis testing : To test a hypothesis that was defined at the outset of the survey design. For instance, in our example we hypothesize that a video ad campaign should have led to changes in key brand perception metrics. It is also commonly used in A/B testing where you compare whether concept A performed better or worse than concept B.
- Exploratory analysis : Surveys often lead to a treasure trove of data. Often the aim is to uncover interesting patterns in the data, such as differences in gender, age, region, relationship status, and other variables. These are anlysed in the form of cross-tabulation tables such one shown below. It is standard practice to run statistical tests across different variables to see where interesting differences lie. Cells that are significant are usually highlighted using colour gradings or letters of the alphabet.
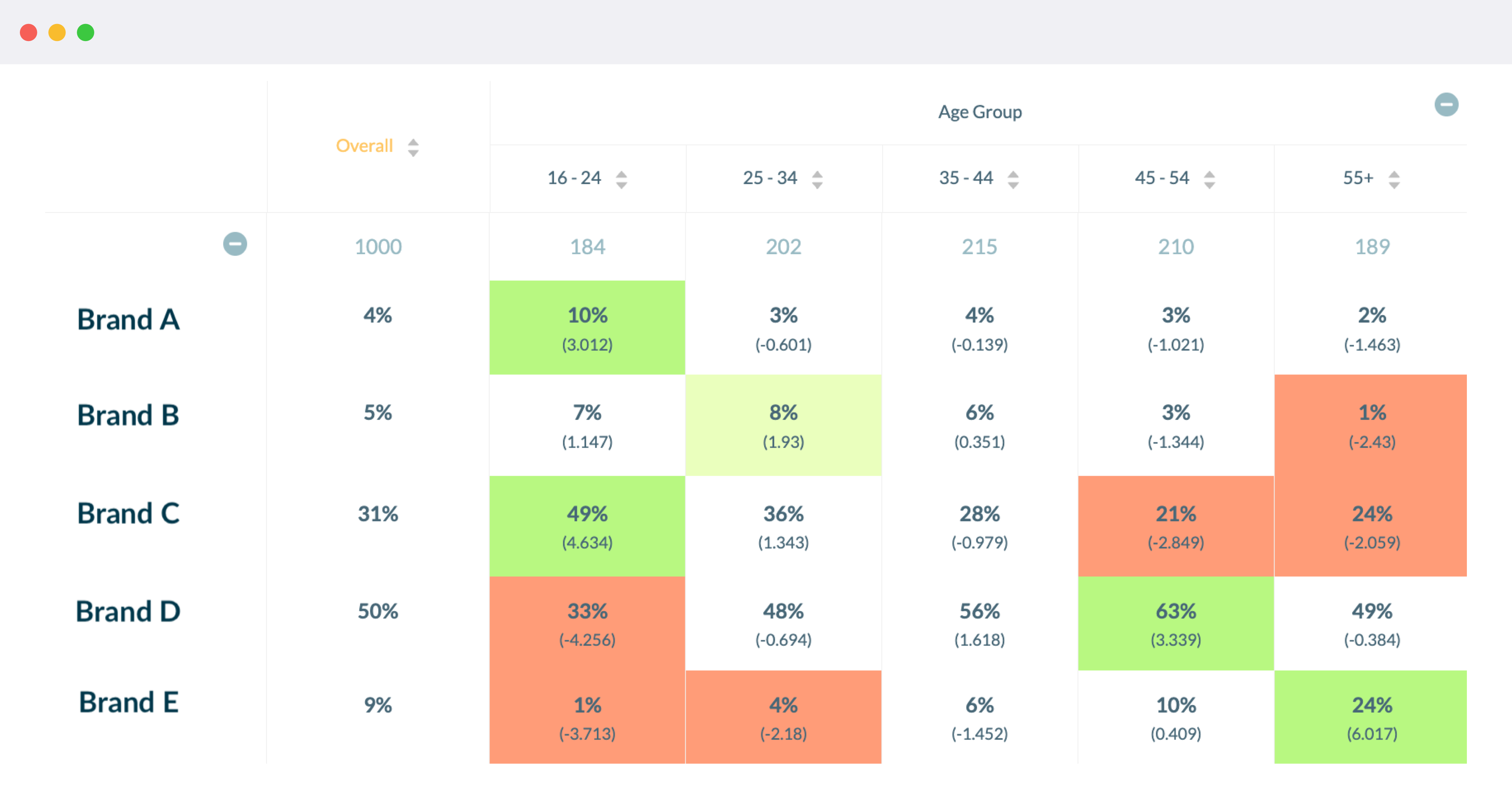
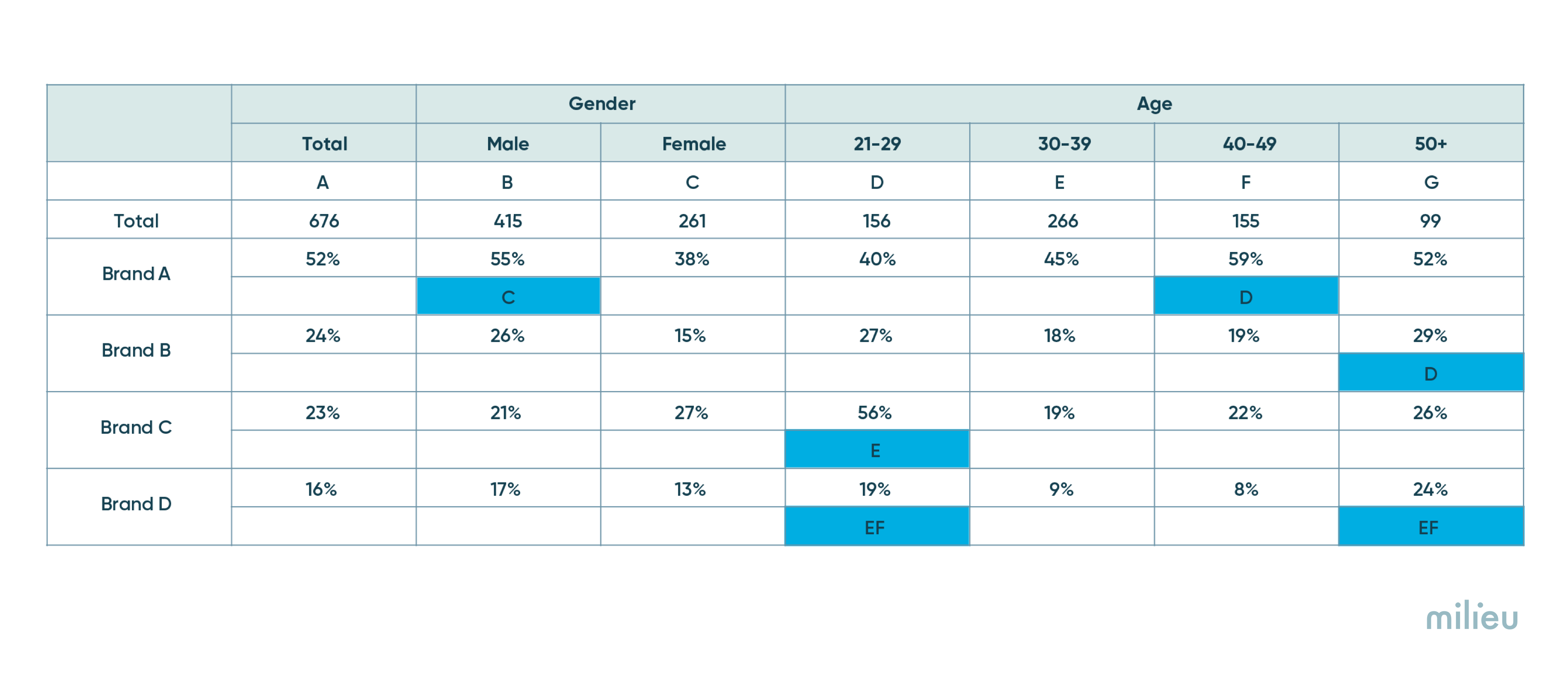
Significance testing can be applied in both the above scenarios. The next sections will highlight the steps involved.
Z-test for proportions and its key steps
Since the data obtained in surveys are typically percentages, z-test for proportions is a common statistical test used to determine whether a difference between two percentages is significant (reflects a real difference in the data), or due to chance. While this article specifically talks about z-test, the theoretical basis behind it is similar to that of other significance testing like t-tests.
Researchers typically use analysis softwares/calculators to do significance tests. In this section we won't take you through the mathematical calculations but instead provide you a theoretical understanding of the what's and why's happening behind the scenes. Below are the key components involved :
1. State your hypothesis
In statistical tests, it is standard practice to state your hypothesis and be clear about what it is that you are testing before you jump into performing the tests. Taking our example of the campaign effectiveness study we can define our hypothesis as follows
Null hypothesis : The first is to establish a null hypothesis, or something you’re trying to disprove. In our case, it would be : There is no meaningful difference in brand awareness before and after the ad campaign.
Alternative hypothesis : An alternate hypothesis is something you’re trying to prove. In our case it would be : The pre and post campaign brand awareness percentages are significantly different i.e. the post campaign brand awareness metric (test group) could be meaningfully lower or greater than the pre-campaign awareness percentage (reference group).
The z-test is basically an evidence gathering exercise : do we have enough evidence to reject the null hypothesis and accept the alternative hypothesis i.e. there is a meaningful difference between the two groups?
As mentioned before, apart from this hypothesis testing, an aim could also be exploratory analysis to uncover interesting differences between other variables. You would follow the same steps for the groups you want to compare. For simplicity, we'll focus on the above hypothesis.
2. Calculating the z-score
The next step involves calculating a z-statistic which is also known as the z-score. Z-score is calculated using a somewhat complex formula but it essentially involves converting raw percentages from our survey results into standard deviation units.
Z-scores can be positive, negative, or equal to zero. The sign indicates whether the test score (post-campaign %) is greater(+) or lower(-) than the reference group (pre-campaign %).
So using our example of a Campaign Effectiveness Study, a z-score of 0 indicates that there is no difference between the pre and post campaign groups. A z-score of +1.5 means that the post-campaign group is 1.5 deviations away from the reference group (pre-campaign group), while a z-score of -0.5 means that the post-campaign group is 0.5 standard deviations lower than the reference group.
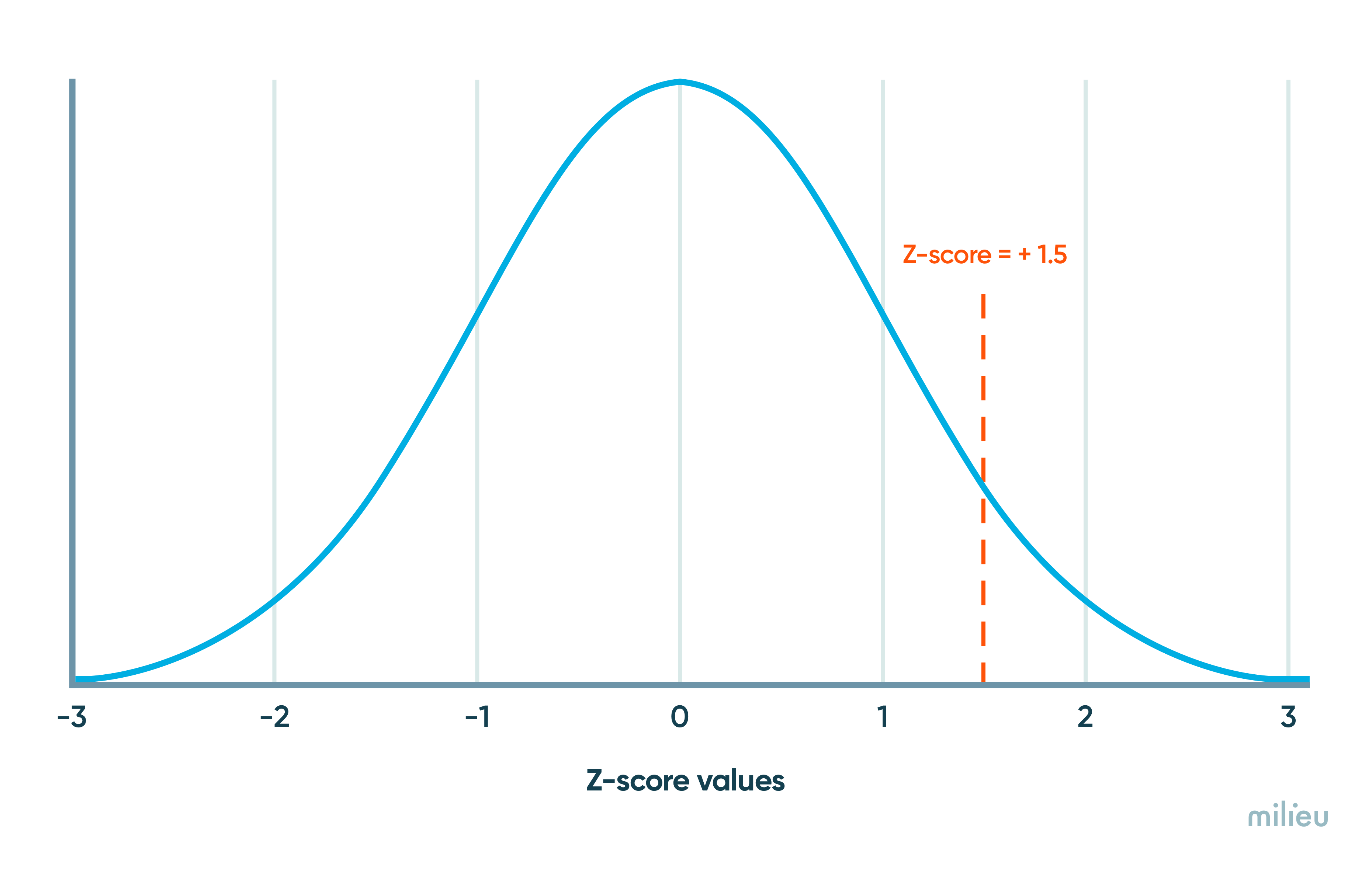
Z-scores are a versatile and powerful tool for data analysis for the following reasons :
1. They enables us to compare two scores from different samples (which may have different means and standard deviations). In our case they enable us to compare % scores from pre and post campaign surveys. Taking raw percentage scores and simply saying there is a x% difference between two groups for a metric is not enough. We need to take into account other factors such as the sample size and standard error for each group, and that’s what z-score does. For example, an 8% difference between two groups is more likely to be statistically significant if their sample sizes were N =1000 than if the sample sizes were much smaller, say N=50.
2. No matter what measurement scale or metric you use, z-scores translate those arbitrary scores into a standardized unit on which a statistical test can be applied. In our case we are using percentage values, but z-tests can be used on a wide variety of metrics such as weight, age, height, exam scores, etc.
3. Z-scores have a probability value attached to them which tells us if the difference is significant or no. This is what is discussed in the next section.
3. Determine your p-value
Every z-score has an associated p-value that tells you the likelihood of the null hypothesis being true or false.
While z-scores measure how many standard deviations a particular data point is from the reference group, p-value is a probability that tells us if the difference you see between the two groups (in the form of z-score) is reliable, or just due to random chance.
Typically, the higher the absolute value of the z-score, the lower the p-value.
- A low p-value shows strong evidence the null hypothesis is NOT true, and can be rejected in favour of the alternative hypothesis. This means that it is very likely that there is a real difference between the groups and not due to random chance.
- A high p-value denotes the statistical evidence is too weak to reject the null hypothesis, and that the null hypothesis is more likely to be true. This means that we cannot be confident that there is a real difference between the two groups, and any difference you see is likely a chance finding.
But what determines what is a low or high p-value? What's the cut-off? And how is it related to the z-score? This is where confidence level comes to play.
4. Specify your Confidence Level
When you read survey results, you might see statements like "The difference was statistically significant at a 95% confidence level."
But what does that mean?
Confidence level is a measure of the reliability or certainty with which we can make inferences about a population based on sample data. Confidence levels are used because, in surveys, we can't interview everyone in our target population, so we only talk to a subset. For example, in our campaign effectiveness survey, we only surveyed 500 people even though there are over 6 million people in Singapore.
A 95% confidence interval means that if we were to replicate our study 100 times, approximately 95 of those repetitions would produce results consistent with our significance test findings.
Confidence levels help you set the threshold in determining whether a z-score yields a significant p-value or not.
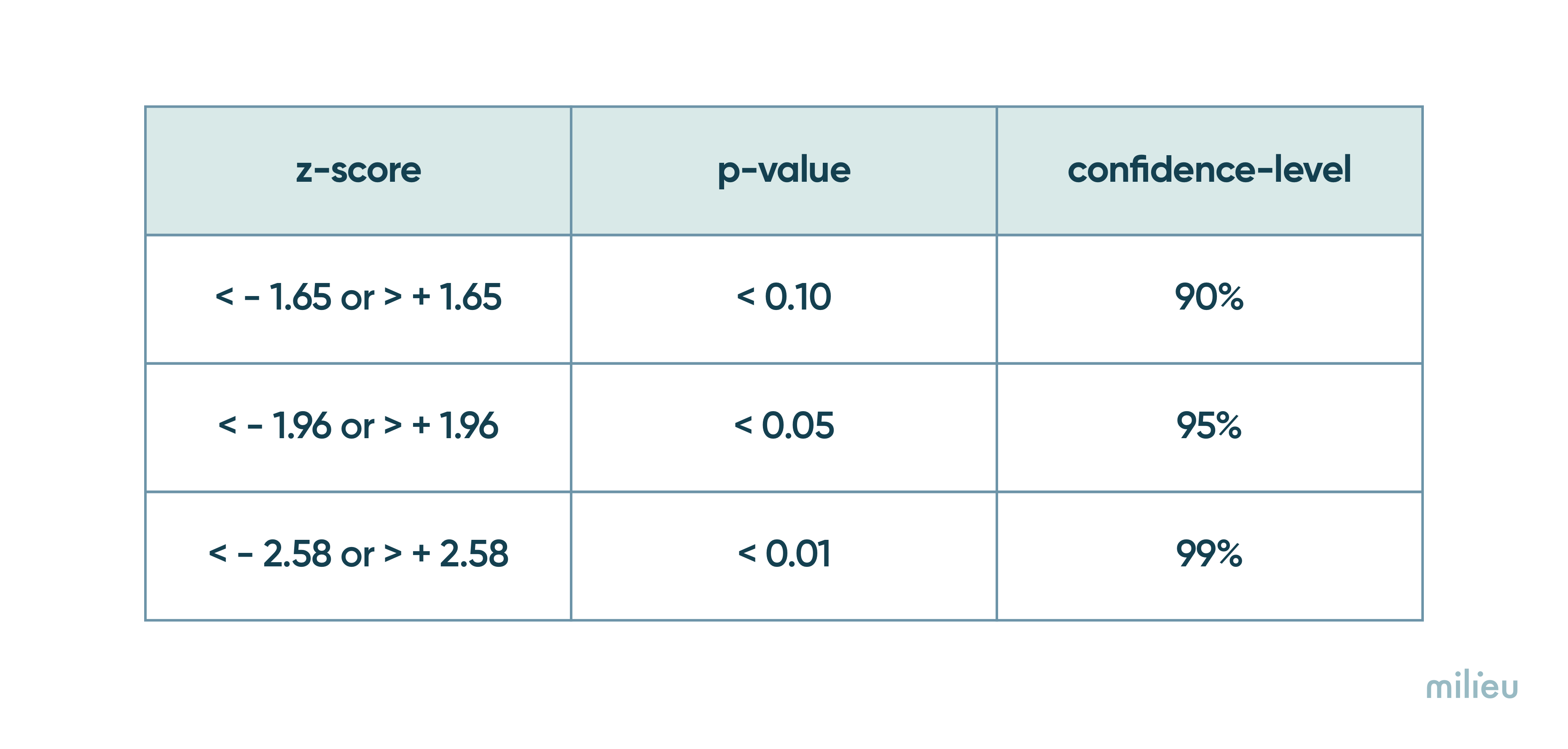
Let’s look at the table below. For a 95% confidence level, the cut-off for significance is at + or - 1.96. This means that if your z-score is greater than 1.96 or less than -1.96 the difference between the two groups is statistically significant (associated with p-value of <0.05).
However, for a 90% confidence level, the cut-off is less stringent. Your z-score needs to be above +1.65 or less than -1.65 (associated with p-value of <0.10) for the difference to be significant. At this confidence level, your z-score has a better chance of being statistically significant however the results can be less precise because at 90% confidence level, we’ll reach the same conclusion 90% of the times instead of 95%.
And it goes without saying to say, for a 99% confidence level, the cut-off is even more strict at +/- 2.58.
The confidence level you choose depends on the implications of your study on decision-making and how precise you need your results to be. If you're changing your product's pricing strategy, you of course want to be as precise as possible, but if you're picking between two design aesthetics you probably willing to be less stringent. It's not a good idea to change your thresholds after the results are in just to force a difference to reach significance. You should ideally decide this at the start.
Limitations of significance testing and how to use it with care
Market research and insights teams use statistical significance to decide whether results from polls, surveys and experiments should impact their business decisions.
However, it is important to recognise and understand the limitations of significance tests so that it is used with good judgement.
1. Sample sizes matter.
One of the main concerns with significance testing is that it is heavily influenced by sample sizes. The underlying presumption is that larger sample sizes are more reliable because it reduces chances of error and minimizes data swings by potential outliers. However, a large sample size can lead to false positives, where even a small and insignificant difference between two groups is deemed statistically significant. Furthermore, there may be instances where real and meaningful difference between groups is missed because the sample is not large enough. This happens a lot with niche target groups.
2. Significance testing should not be the only lens through which you look at your data.
The below excerpt from Esomar opines :
"Statistical significance is a binary idea in a world shaded by gray.
While people may be tempted to blur the line when calls are close, significance testing is a binary idea. A p-value is either significant or it is not. You can, of course, grade on a curve by setting the threshold you want to achieve, but because the test is designed to reflect sample size as much as magnitude of difference, there is often a painful arbitrariness to the outcome. A statistical difference deemed significant with n=100 might fail to qualify as significant with just n=99."
This is a reminder that statistical significance is not a black-and-white test. It is important to consider other factors, such as the magnitude of the effect, the sample size, and the context of the study, when interpreting the results of a statistical test.
3. The p-value is sometimes not enough. One can consider using effect sizes.
A lower p-value is often seen as an evidence for a stronger relationship between two variables. However, that is not true. It merely tells us that the probability of the null hypothesis being true is very unlikely (p-value < 0.05 means the probability is less than 5%).
In the context of survey-driven decision making, it is not only helpful to know whether results have a statistically significance, but also what is the the size of the observed difference.
An effect size tells us that. A significant p-value tells us there is a meaningful difference, whereas an effect size tells us the magnitude or strength of the difference, allowing us to decide if the difference is substantial enough.
Cohen’s h is a frequently used statistic used to describe the difference between two proportions as "small", "medium", or "large".
Large effect h >= 0.80
Medium effect h >= 0.50
Small effect h >= 0.20
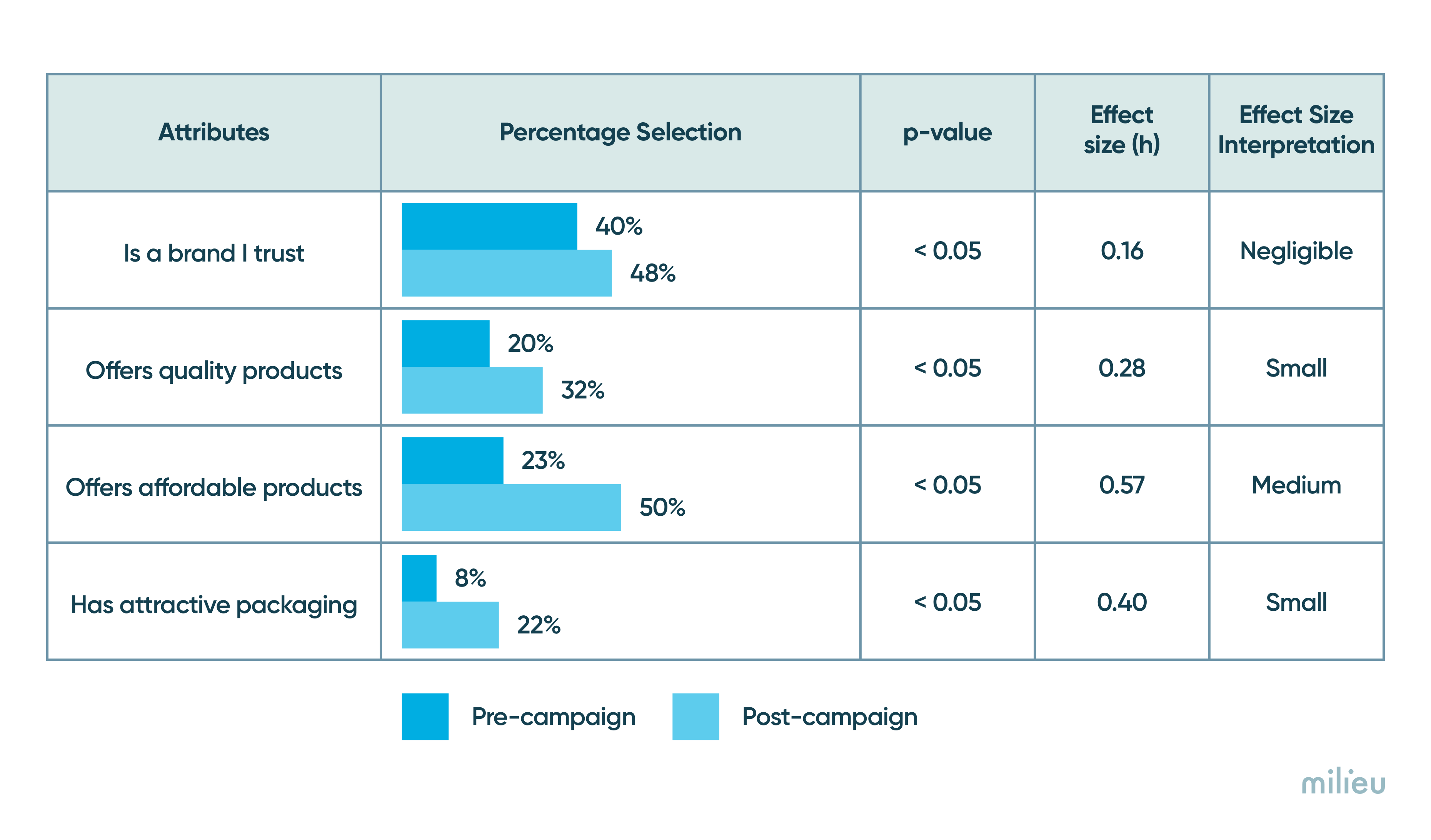
4. If the findings of your study have practical implications, don't prevent a significance testing from telling you otherwise.
For instance, here is an example from a Harvard Business Review article that provides a practical example :
"[say] a new marketing campaign produced a $1.76 boost (more than 20%) in average sales. It’s surely of practical significance. If the p-value comes in at 0.03 the result is also statistically significant, and you should adopt the new campaign. If the p-value comes in at 0.2 the result is not statistically significant, but since the boost is so large you’ll likely still proceed, though perhaps with a bit more caution.
But what if the difference were only a few cents? If the p-value comes in at 0.2, you’ll stick with your current campaign or explore other options. But even if it had a significance level of 0.03, the result is likely real, though quite small. In this case, your decision probably will be based on other factors, such as the cost of implementing the new campaign."
We hope you found this article useful. Here's to using statistical tests with a better understanding and responsibility.
Feel free to check out more articles on concepts related to market research on our Learn Section.
If you have questions related to Milieu's survey platform and/or other product/service offerings feel free to reach out to sales@mili.eu.

Author
Antarika Sen
Latest Insights

.avif)


.webp)

